前言
MIT 18.06,之前看过,但是都忘了,所以这回快速的复习一下,记好一些的笔记,要做题!
重振小镇做题家之荣耀,我辈义不容辞!
https://mitmath.github.io/1806/

贴一张老爷子的照片,感谢!
1. 方程组的集合解释
线性代数:求解方程组
$$\begin{cases}& 2x - y =0 \\ &-x + 2y = 3 \end{cases} \rightarrow \begin{bmatrix} 2 &-1 \\ -1 &2 \end{bmatrix} \begin{bmatrix}\bold{x} \\\bold{y} \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \rightarrow AX=B $$
行图像 (Row picture)

两条直线的交点就是这个方程组的解
列图像 (Column picture)
$$ \begin{bmatrix} 2 &-1 \\ -1 &2 \end{bmatrix} \begin{bmatrix} \bold{x} \\ \bold{y} \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}\rightarrow x \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \rightarrow Ax=b$$
这个方程的目的就是找到合适的$x$和$y$使得前两个向量组合可以得到后一个向量 [也就是找到正确的线性组合],这里是列向量的线性组合

新的问题:对于任意的b(右侧向量),是否都能求解$Ax=b$
也就是:列的线性组合能否覆盖整个空间?
矩阵
方程的矩阵形式:
$$Ax=b$$
矩阵A乘以向量x得到右侧的向量b
矩阵和向量的乘法的两种解:
使用列图像进行乘法(推荐)
矩阵的每一列都看成是一列向量,外部的向量b其实就是每一列向量的系数
或者可以将矩阵的每一列看成一个空间的基地,外部的向量b就是根据这个基地在每个方向上的长度
$$ \begin{bmatrix} 2 &5 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1\\2 \end{bmatrix} = 1 \begin{bmatrix} 2\\ 1 \end{bmatrix} + 2 \begin{bmatrix} 5\\ 3 \end{bmatrix} =\begin{bmatrix} 12\\ 7 \end{bmatrix} $$
- 使用行图像进行计算
$$ \begin{bmatrix} 2 &5 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} =12 $$
2. 消元法求解线性方程组
消元得到上三角矩阵
$$ \begin{cases} x+ &2y+ &z &=2 \\ 3x+ &8y+ &z &=12 \\ &4y+ &z &=2 \end{cases} \rightarrow Ax=b \qquad A=\begin{bmatrix} 1 &2 &1 \\ 3 &8 &1 \\ 0 &4 &1 \end{bmatrix} $$
按顺序进行消元,对角线上的元素称为主元(pivot),因为需要使用对角线上的元素迭代的消去下面等式中的对应元素。但是0不能作为主元
$$ A= \begin{bmatrix} 1 &2 &1 \\ 3 &8 &1 \\ 0 &4 &1 \end{bmatrix} \stackrel{(2,1)}{\rightarrow} \begin{bmatrix} 1 &2 &1 \\ 0 &2 &-2 \\ 0 &4 &1 \end{bmatrix} \stackrel{(3,2)}{\rightarrow} \begin{bmatrix} 1 &2 &1 \\ 0 &2 &-2 \\ 0 &0 &5 \end{bmatrix} = U$$
箭头上方表示想要消去的元素的位置
这里消元的目的就是为了从$A$得到上三角矩阵$U$.
消元法失效
如果主元是0的时候,需要进行行交换,让非0元素占据主元的位置。
如果行交换无法使主元是非0元素,那么这个方程就没有解,这个矩阵也就是不可逆的。
回代
当使用消元法从$A$得到$U$之后,就需要把右侧向量$b$带入,引入$b$作为新的一列向量加入到矩阵中,也就是增广矩阵
$$ \begin{bmatrix} 1 &2 &1 &2 \\ 3 &8 &1 &12 \\ 0 &4 &1 &2 \end{bmatrix} $$
因为对左侧矩阵进行变化的同时,右侧向量也会跟着做同样的变化,所以按照上面的消元法:
$$ \begin{bmatrix} 1 &2 &1 &2 \\ 3 &8 &1 &12\\ 0 &4 &1 &2 \end{bmatrix} \stackrel{(2,1)}{\rightarrow} \begin{bmatrix} 1 &2 &1 &2 \\ 0 &2 &-2 &6 \\ 0 &4 &1 &2 \end{bmatrix} \stackrel{(3,2)}{\rightarrow} \begin{bmatrix} 1 &2 &1 &2 \\ 0 &2 &-2 &6 \\ 0 &0 &5 &-10 \end{bmatrix} \rightarrow c=\begin{bmatrix} 2 \\ 6 \\ -10\end{bmatrix}$$
所以最终方程的形式是这样的:
$$\begin{cases} x+ &2y+ &z &=2 \\ &2y- &2z &=6 \\ & &5z &=-10\end{cases}\rightarrow Ux=c$$
接下来进行回代求解:$z=-2; y=1; x=2$
矩阵形式描述消元法
使用行进行计算
$$ \begin{bmatrix} 1 &2 &7 \end{bmatrix} \begin{bmatrix} 2 & 3 & 4 \\ 1 & 3 & 4 \\ 2 & 3 & 5 \end{bmatrix} = \begin{bmatrix}2 &3 &4\end{bmatrix}\times 1 + … + \begin{bmatrix}2 &3 &5\end{bmatrix}\times 7 = \begin{bmatrix}18 &30 &47\end{bmatrix} $$
左行右列,左乘行变换,右乘列变换
- 列向量是乘在矩阵的右边,对矩阵的每一列进行线性合并,得到的是列向量
- 行向量是乘在矩阵的左边,对矩阵的每一行进行线性合并,得到的是行向量
消元矩阵
$$\begin{bmatrix} 1 &2 &1 \\ 3 &8 &1 \\ 0 &4 &1 \end{bmatrix} \stackrel{(2,1)}{\rightarrow} \begin{bmatrix} 1 &2 &1 \\ 0 &2 &-2 \\ 0 &4 &1 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 &0 &0 \\ -3 &1 &0 \\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &2 &1 \\ 3 &8 &1 \\ 0 &4 &1 \end{bmatrix} = \begin{bmatrix} 1 &2 &1 \\ 0 &2 &-2 \\ 0 &4 &1 \end{bmatrix}$$
原来的消元法就变成了一个特定的矩阵:消元矩阵
$$E_{21} = \begin{bmatrix} 1 &0 &0 \\ -3 &1 &0 \\ 0 &0 &1 \end{bmatrix}$$
他的每一行都是对矩阵的行变换,同时也被称为初等矩阵$E$,因为是对(2,1)位置上进行消元,所以可以写成$E_{21}$
所以,整个过程使用矩阵形式表达:
$$E_{32}(E_{21}A)=U$$
矩阵乘法满足结合律,所以可以将括号移动,变成一个矩阵,来实现所有的消元任务。但是矩阵乘法不满足交换律,不可轻易调换他们的顺序
$$(E_{32}E_{21})A=U$$
置换矩阵 (pemutation)
对行进行调换:
$$ \begin{bmatrix} 0 &1 \\ 1 &0 \end{bmatrix} \begin{bmatrix} a &b \\ c &d \end{bmatrix} = \begin{bmatrix} c &d \\ a &b \end{bmatrix} $$
其中,$P=\begin{bmatrix} 0 &1 \\ 1 &0\end{bmatrix}$就是置换矩阵,将两行进行位置的调换
同理,如果想对列进行置换,那么需要将矩阵进行右乘,左行右列
可以看到,因为想要消除置换矩阵带来的影响,那就是把它再置换回去,那么置换矩阵的逆就是置换矩阵的转置
$$P^{-1}=P^{T}$$
分清转置(T,是一个操作) 和 置换(P,是一个矩阵),两个不一样的东西
矩阵的逆
$$\begin{bmatrix} 1 &0 &0 \\ -3 &1 &0 \\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &2 &1 \\ 3 &8 &1 \\ 0 &4 &1 \end{bmatrix} = \begin{bmatrix} 1 &2 &1 \\ 0 &2 &-2 \\ 0 &4 &1 \end{bmatrix}$$
初等矩阵$E_{21} = \begin{bmatrix} 1 &0 &0 \\ -3 &1 &0 \\ 0 &0 &1 \end{bmatrix}$,从行2中减去了三倍的行1,现在我想回做这一步,也就是找到某一个矩阵取消这次消元(左乘),即两者相成为单位阵$I$:
$$E^{-1}_{21}E_{21}=I$$
那么对于$E_{21}$来说,他的含义相当于是从行2减去了三倍的行1,那么想消去这个行变换的影响,就应该让行2加回来三倍的行1,所以
$$E^{-1}_{21}=\begin{bmatrix} 1 &0 &0 \\ 3 &1 &0 \\ 0 &0 &1 \end{bmatrix}$$
3. 矩阵的乘法和逆
矩阵乘法
矩阵乘法:$AB=C$
点乘法
其中矩阵$C$的3行4列的元素$C_{34}=A_{row-3}\cdot B_{col-4}=\sum_{k=1}^{n}{a_{3k}b_{k4}}$
列向量法
$$A_{m\times n}B_{n\times p} = C_{m\times p}$$
可以将乘法考虑成一个矩阵右乘以一个列向量,得到一个列向量。也就是矩阵A右乘矩阵B中的每一个列向量
那么,矩阵C的各列是矩阵A中各列的线性组合
行向量法
与列向量法类似,可以将乘法考虑成矩阵B左乘矩阵A中的行向量,
矩阵C的各行是矩阵B中各行的线性组合
列 X 行
常规方法中,是A的行$\times$B的列,得到是相对应位置的标量
但是这里可以是A的列$\times$B的行
$AB$是A的各列$\times$B的各行的矩阵的和
分块乘法
将矩阵进行分块,对每一个分块进行乘法
$$ \begin{bmatrix} A_{1} & A_{2} \\ A_{3} & A_{4} \end{bmatrix} \begin{bmatrix} B_{1} & B_{2} \\ B_{3} & B_{4} \end{bmatrix} = \begin{bmatrix} A_{1}B_{1} + A_{2}B_{3} & A_{1}B_{2}+A_{2}B_{4} \\ A_{3}B_{1} + A_{4}B_{3} & A_{3}B_{2}+A+{4}B_{4} \end{bmatrix} $$
矩阵的逆 (Inverse)
只考虑方阵(square matrix) $A$
逆是否存在
如果存在,可以成立:$A^{-1}A=I$,$I$为单位阵
其中,这里的是左逆,也可以有右逆,表达为:$AA^{-1}=I$
对于方阵,左逆=右逆,即$A^{-1}A=I=AA^{-1}$
如果逆存在,那么矩阵A是可逆的,也就是非奇异的(non-singular)
奇异矩阵
如果存在非0向量$x$使得$Ax=0$,那么这个矩阵$A$是奇异的
也就是其实在矩阵A中的列向量,最少有一对向量是共平面的
可逆矩阵
求矩阵的逆:
$$ \begin{bmatrix} 1 & 3 \\ 2 &7 \end{bmatrix} \begin{bmatrix} a & c \\ b &d \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 &1 \end{bmatrix} \rightarrow AA^{-1}=I $$
Gauss-Jordan:同时处理两个方程组
对增广矩阵($[AI]$)进行消元,得到$E[A|I]=[EA|EI]=[I|E]$,那么$E$就是$A^{-1}$
$$ \begin{bmatrix} \begin{array}{cc|cc} 1 & 3 & 1 & 0 \\ 2 &7 & 0 & 1 \end{array} \end{bmatrix} \rightarrow \begin{bmatrix} \begin{array}{cc|cc} 1 & 3 & 1 & 0 \\ 0 &1 & -2 & 1 \end{array} \end{bmatrix} \rightarrow \begin{bmatrix} \begin{array}{cc|cc} 1 & 0 & 7 & -3 \\ 0 &1 & -2 & 1 \end{array} \end{bmatrix} $$
矩阵乘积的逆
$A$和$B$都是可逆矩阵,那么他们乘积的逆是$(AB)^{-1}=B^{-1}A^{-1}$
逆和转置
对于单个方阵,转置和逆可互换操作
$$(A^{-1})^{T} = (A^{T})^{-1}$$
4. 矩阵A的LU分解
考虑三维矩阵,对A进行消元得到U,即
$$E_{32}E_{31}E_{21}A=U$$
可以写成$A=LU$形式,即:
$$A=E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}U$$
其中U表示的上三角矩阵,L表示的下三角矩阵
$$ \begin{cases} A = LU \\ EA=U \end{cases} $$
下面讨论这两种形式,为什么要变成$A=LU$的形式
对于$A=LU$如果不存在行互换,消元乘数可以直接写进$L$里面
举个例子
$$ E_{32}=\begin{bmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 & -5 &1 \end{bmatrix} E_{31} = I \quad E_{21}=\begin{bmatrix} 1 &0 &0 \\ -2 &1 &0 \\ 0 &0 &1 \end{bmatrix} $$
对矩阵进行消元,进行上述消元变化:$E_{21}$和$E_{32}$
$$ E=E_{32}E_{31}E_{21} = \begin{bmatrix} 1 &0 &0 \\ -2 &1 &0 \\ 10 &-5 &1 \end{bmatrix} $$
这种形式下可以看到行1通过行2影响到了行3,在(1,3)位置出现了10
$$ L = E_{21}^{-1}E_{32}^{-1}= \begin{bmatrix} 1 &0 &0 \\ 2 &1 &0 \\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 & 5 &1 \end{bmatrix} = \begin{bmatrix} 1 &0 &0 \\ 2 &1 &0 \\ 0 &5 &1 \end{bmatrix} $$
在这种形势下,2和5不会冲突产生10,也就是消元乘数可以直接写到$L$里
5. 置换、转置与向量空间
置换 (Permutation, $P$)
置换矩阵是行重新排列了的单位矩阵,是用来完成行互换的矩阵
对于需要进行置换操作的消元,$A=LU$就会变成了$PA=LU$
所有的置换矩阵都是可逆的,并且$P^{T} = P^{-1}$
对于n维方阵,共有$n!$个置换矩阵
转置 (Transpose)
$(A^{T})_{ij}=A_{ji}$
对称矩阵 (symmetric)
对称矩阵:转置变换以后,没有变化的矩阵 $A^{T}=A$
所有的矩阵R转置乘以R都是对称的
$$ \begin{bmatrix} 1 &3 \\ 2 &3 \\ 4 &1 \end{bmatrix} \begin{bmatrix} 1 &2 &4 \\ 3 &3 &1 \end{bmatrix} = \begin{bmatrix} 10 &11 &7 \\ 11 &13 &11 \\ 7 &11 &17 \end{bmatrix} $$
证明:
$$(R^{T}R)^{T} = R^{T}R$$
向量空间
空间:满足加法和数乘(即可以进行线性运算),比如: $\mathbb{R}^{2}$,表示所有的二维实向量。(二维:即向量用两个实数表述)
$$ \begin{bmatrix} 3 \\ 2 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \pi \\ e \end{bmatrix}, \cdots $$
$\mathbb{R}^{n}$包含所有的n维实向量
子空间:需要满足线性运算,但同时又是空间的子集,比如$\mathbb{R}^{2}$的子空间:
- $\mathbb{R}^{2}$本身
- 所有经过原点的直线
- (0,0)点
列空间
从矩阵中构造一个子空间:
$$A=\begin{bmatrix} 1 &3 \\ 2 &3 \\ 4 &1 \end{bmatrix}$$
矩阵A的所有列都在$\mathbb{R}^{3}$空间中,他的列的所有线性组合都成一个子空间:列空间,记作$C(A)$
6. 列空间和零空间
向量空间:一些向量组成的空间,对加法和数乘运算封闭
有子空间$S$和$T$,他们的交集$S\cap T$仍是子空间
列空间
$$ A=\begin{bmatrix} 1 &1 &2 \\ 2 &1 &3 \\ 3 &1 &4 \\ 4 &1 &5 \\ \end{bmatrix} $$
矩阵A的列看做向量,那么矩阵A的列空间是$\mathbb{R}^{4}$的子空间,记作$C(A)$
$C(A)$由这三个列向量线性组合的所有向量构成,因为矩阵A的三个列向量不是线性无关的,所以$C(A)$是$\mathbb{R}^{4}$中的二维子空间
下面开始讨论这个子空间有“多大”,并将它和线性方程组$Ax=b$联系起来,即
$Ax=b$是否对任意的$b$都有解,满足什么条件的$b$可以满足$Ax=b$
$Ax=b$有解当且仅当$b\in C(A)$
零空间
$A$的零空间包含$Ax=0$中所有的解$x=\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3}\end{bmatrix}$,对于矩阵$A$,他的零空间属于$\mathbb{R}^{3}$
$Ax=0$的特解:
$$ \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 \\ 1 \\ -1 \end{bmatrix} $$
所以A的零空间包含了$c\begin{bmatrix} 1 \\ 1 \\ -1\end{bmatrix}$
所以A的零空间就是$\mathbb{R}^{3}$中的一条直线
7. 求解零空间Ax=0
之前讲过了列空间和零空间的基本概念,现在主要关注的是如何去求解列空间和零空间
$$ A=\begin{bmatrix} 1 &2 &2 &2 \\ 2 &4 &6 &8 \\ 3 &6 &8 &10 \end{bmatrix} $$
下面通过消元来求解$Ax=0$,消元并不会改变$Ax=0$的解
$$ A=\begin{bmatrix} 1 &2 &2 &2 \\ 2 &4 &6 &8 \\ 3 &6 &8 &10 \end{bmatrix} \rightarrow \begin{bmatrix} 1 &2 &2 &2 \\ 0 &0 &2 &4 \\ 0 &0 &2 &4 \end{bmatrix} \rightarrow \begin{bmatrix} \colorbox{yellow}{\color{red}{1}} &2 &\colorbox{yellow}{2} &2 \\ \colorbox{yellow}{0} &0 &\colorbox{yellow}{\color{red}{2}} &4 \\ \colorbox{yellow}{0} &0 &\colorbox{yellow}{0} &0 \end{bmatrix}=U $$
最终得到了这种矩阵的阶梯形式(echelon form),非零元素以一种阶梯形式出现。其中红色表示的就是矩阵的主元(pivots)
矩阵主元的个数称为该矩阵的秩(rank)
现在从$Ax=0$变换到了$Ux=0$,他的解没有变,也就是零空间没有变
所以下面通过$U$来求解$A$的零空间
主元所在列称为主列(pivot column),也就是矩阵中的黄色部分;其他的列称为自由列(free columns)
自由列表示可以任意、自由的分配数值;列2和列4的乘数是任意的,即可以任意的分配$x_{2}$和$x_{4}$。当$x_{2}$和$x_{4}$固定下来,$x_{1}$和$x_{3}$随之固定
所以需要任意假定一个$x_{2}$和$x_{4}$数值,但是因为零向量肯定是零空间中的一个解,所以把自由列所对应的元素全假定成0没有意义,这里一般是采用one-hot想法,逐一假设成1来进行求解(这里的解应该是零空间的特解)
$$ x_{2}=1,x_{4}=0 \Rightarrow \begin{bmatrix} -2 \\ 1 \\ 0 \\ 0 \end{bmatrix};x_{2}=0,x_{4}=1 \Rightarrow \begin{bmatrix} 2 \\ 0 \\ -2 \\ 1 \end{bmatrix} $$
所以,$Ax=0$的解就是
$$ c_{1}\begin{bmatrix} 2 \\ 0 \\ -2 \\ 1 \end{bmatrix}+ c_{2}\begin{bmatrix} -2 \\ 1 \\ 0 \\ 0 \end{bmatrix} $$
如果矩阵$A_{m\times n}$的秩$r=2$,表示只有r个方程起作用。他的自由列、自由变量就有$n-r$个,可以采用one-hot形式进行取值,得到特解
可以看到,使用列向量来理解整个矩阵、方程组的求解,理解将会变得非常的顺畅
下面继续对行阶梯形式的$U$进行再一次的简化,得到的简化行阶梯形式记为$R$ (Reduced row echelon form)。而简化行阶梯形式主元上下全是0,主元为1
$$U=\begin{bmatrix} 1 & 2 & 2 & 2 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & 0 & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 2 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix}=R$$
简化行阶梯形式$R$中包含了这些信息:
$$ R=\begin{bmatrix} \colorbox{yellow}{1} & 2 & \colorbox{yellow}{0} & -2 \\ \colorbox{yellow}{0} & 0 & \colorbox{yellow}{1} & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \stackrel{col2\iff col3}{\longrightarrow} \begin{array}{l} \begin{bmatrix} \colorbox{yellow}{1} & \colorbox{yellow}{0} &\colorbox{pink}{2} & \colorbox{pink}{-2} \\ \colorbox{yellow}{0} & \colorbox{yellow}{1} &\colorbox{pink}{0} & \colorbox{pink}{2} \\ \colorbox{orange}{0} & \colorbox{orange}{0} &\colorbox{orange}{0} &\colorbox{orange}{0} \end{bmatrix}\\ \quad c_{1} \quad c_{3} \quad c_{2} \quad c_{4} \end{array} \rightarrow \begin{bmatrix} \colorbox{yellow}{I} \colorbox{pink}{F} \\ \colorbox{orange}{0\quad 0} \end{bmatrix} $$
其中$I_{r\times r}$,自由列$F_{r\times n-r}$
在经过列变换后,我们再求$Rx=0$的解
构造零空间矩阵:他的各列由特解组成,记为$N$,即满足$RN=0$
那么通过上面列变换之后的简化行阶梯形式,我们可以很容易得到
$$N=\begin{bmatrix} -F \\ I\end{bmatrix}=\begin{bmatrix} -2 & 2 \\ 0 & -2 \\ 1 &0 \\ 0 &1\end{bmatrix}$$
再把相应的行2和行3调换回去就可以了,就得到了之前得到的特解
8. 求解Ax=b
有了前面的铺垫,现在正是进入到求解线性方程组。
线性代数的根本目的就是为了求解线性方程组
$$ A=\begin{bmatrix} 1 &2 &2 &2 \\ 2 &4 &6 &8 \\ 3 &6 &8 &10 \end{bmatrix} \Rightarrow \begin{cases} x_{1} +&2x_{2}+&2x_{3}+&2x_{4} = b_{1} \\ 2x_{1}+&4x_{2}+&6x_{3}+&8x_{4} = b_{2} \\ 3x_{1}+&6x_{2}+&8x_{3}+&10x_{4} = b_{3} \end{cases} $$
考虑$Ax=b$的增广矩阵$[A|b]$:
$$ \begin{bmatrix} \begin{array}{cccc|c} 1 &2 &2 &2 &b_{1} \\ 2 &4 &6 &8 &b_{2} \\ 3 &6 &8 &10 &b_{3} \end{array} \end{bmatrix} $$
同上进行消元
$$ \begin{bmatrix} \begin{array}{cccc|c} 1 &2 &2 &2 &b_{1} \\ 0 &0 &2 &4 &b_{2}-2b_{1} \\ 0 &0 &0 &0 &b_{3}-b_{2}-b_{1} \end{array} \end{bmatrix} $$
所以有解的条件就是$b_{3}-b_{2}-b_{1}=0$,因为第三个方程左边全是0
可解性
$Ax=b$有解,当且仅当$b$属于$A$的列空间时
由上面的$Ax=b$的求解过程可知,换一种表述为:
如果$A$各行的线性组合得到零行,那么$b$中元素的同样组合必然也是零,就像$b_{3}-b_{2}-b_{1}$
求Ax=b的所有解
第一步只求一个特定的解,即特解(particular solution)
其中一个方法就是,把所有的自由变量设为0,求出$Ax=b$的主变量
按照上面进行举例: $x_{2}=0, x_{4}=0$可以得到
$$\begin{cases} x_{1} +2x_{3} =1 \\ 2x_{3}=3 \end{cases} $$
可得:$x_{1}=-2, \quad x_{3}=\frac{3}{2}$,特解向量为$x_{p}=\begin{bmatrix}-2 \\ 0 \\ \frac{3}{2} \\ 0 \end{bmatrix}$
第二步,求解$A$的零空间$x_{n}$
最终的解就是特解加上零空间中的任意向量$x=x_{p}+x_{n}$
因为$Ax_{p}=b$,$Ax_{n}=0$
使用秩讨论Ax=b的求解
对于$m\times n$的矩阵$A_{m\times n}$,他的秩是$r$ ($r\le m, r\le n$)
列满秩 (r=n<m)
每一列都有主元,没有自由变量。
这个时候$A$的零空间只有零向量$N(A) = \{ 0\}$
如果$Ax=b$有解,只存在一个解,就是特解,即$x=x_{p}$
行满秩 (r=m<n)
这种情况下,将会得到$m$个主元,这个时候通过消元法我们可知不会出现零行,所以对于任意的$b$,$Ax=b$都有解
自由变量为$n-r$个
举个例子,有点不好理解
$$A=\begin{bmatrix} 1 &2 &6 &5 \\ 3 &1 &1 &1\end{bmatrix}$$
矩阵的秩是2,得到的简化阶梯型:
$$R=\begin{bmatrix} 1 &0 &\_ &\_ \\ 0 &1 &\_ &\_ \end{bmatrix}$$
$R$中没有零行,左边是单位阵,右边就是自由变量组成的矩阵$F$,可以任意设定
满秩 (r=m=n)
这种矩阵肯定是方阵,他是可逆矩阵,简化阶梯型$R=I$,零空间只有0向量,$Ax=b$有且只有唯一解
矩阵的秩决定了方程组解的数目
9. 线性相关、向量空间的基和维数
“向量组”是线性相关、无关;“向量组”生成一个空间;“向量组”作为一组基
他们都是针对的向量组进行讨论,而不是矩阵
线性无关
什么条件下,向量$x_{1}, x_{2}, \cdots, x_{n}$是线性无关的?
如果不存在结果为零向量的组合,则向量组线性无关(除非系数全0)
当向量$x_{1}, x_{2}, \cdots, x_{n}$是矩阵$A$的列向量,如果矩阵$A$的零空间只存在零空间,那么这个向量组线性无关,即这个矩阵$A$的秩$r=n$
向量空间
设向量组$v_{1},v_{2},\cdots,v_{l}$生成(span)了一个向量空间,表示这个空间包含了这些向量的所有线性组合
向量空间的基:指一系列的向量$v_{1},v_{2},\cdots,v_{d}$,他们线性无关、可以生成整个向量空间
对于给定空间,$\mathbb{R}^{2},\mathbb{R}^{n},…$,空间中基的个数是相等的,即空间的维度
$$ A=\begin{bmatrix} 1 &2 &3 &1 \\ 1 &1 &2 &1 \\ 1 &2 &3 &1 \end{bmatrix} $$
他的列空间$C(A)$,前两列向量就是这个列空间的基,那么这个列空间的维数就是矩阵$A$的秩。
(注意,这里说的不是矩阵$A$的维度,而是矩阵$A$的列空间的维度!)
零空间表达是这些向量组怎么线性相关的,零空间的维度是$dim N(A) = n-r$
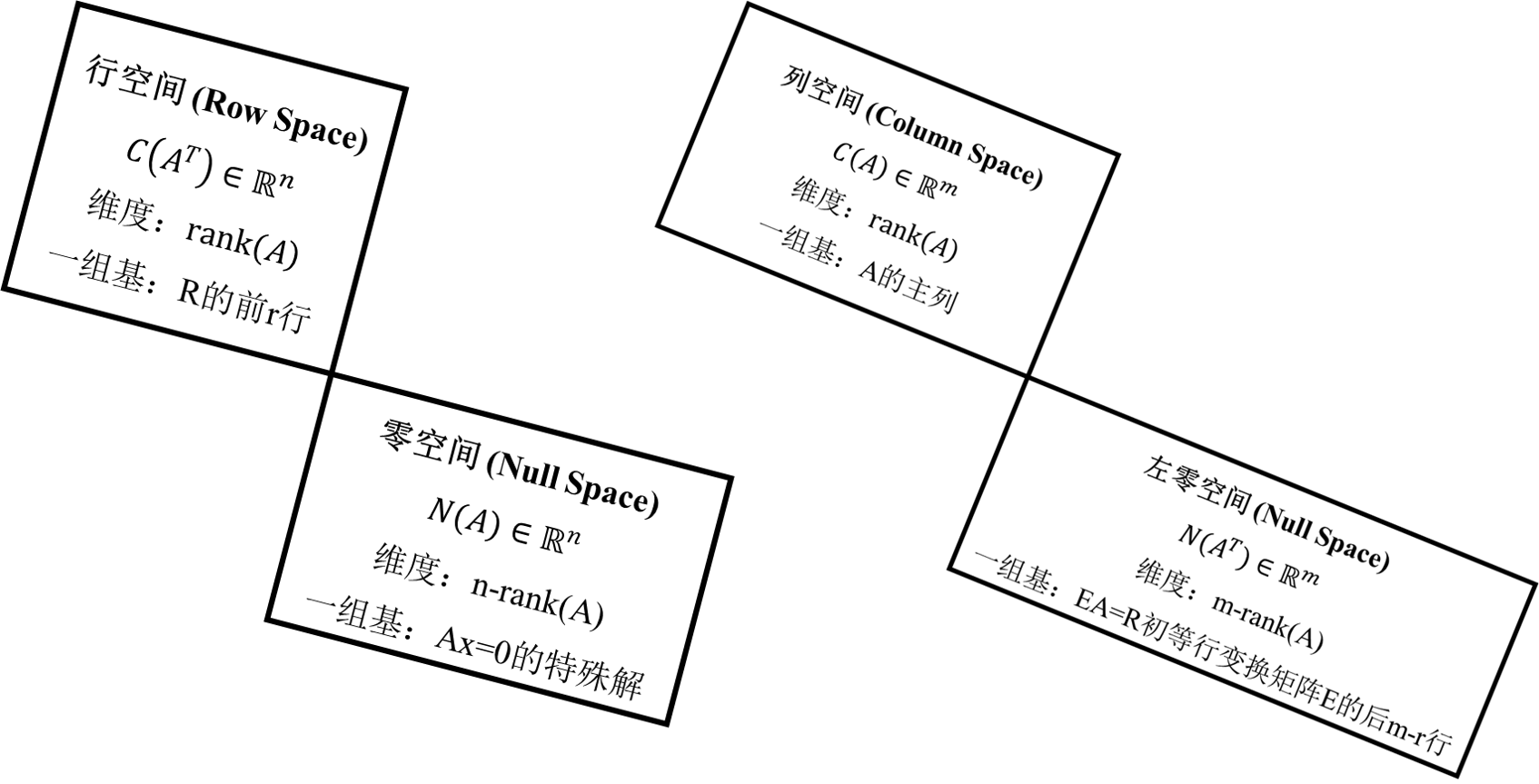
10. 矩阵的四个基本子空间
对于矩阵$A_{m\times n}$
列空间$C(A)\in \mathbb{R}^{m}$
零空间$N(A)\in \mathbb{R}^{n}$
行空间$C(A^{T}) \in \mathbb{R}^{n}$: 矩阵$A$转置的列的所有线性组合
因为一般不太喜欢处理行向量,所以进行转置之后处理列向量。爱的魔力转圈圈~~~
- 左零空间$N(A^{T})\in \mathbb{R}^{m}$
关心这些空间的一组基,以及他们的维数
| 子空间 | 维度 | 一组基 |
|---|---|---|
| 列空间 | 矩阵$A$的秩$rank(A)$ | 矩阵$A$的r个主列 (注意这里是矩阵$A$,不是$U$或是$R$) |
| 行空间 | 矩阵$A$的秩$rank(A)$ | 行最简矩阵$R$的前r行 |
| 零空间 | $n-r$ | $Ax=0$得到的特殊解 (每个自由变量都可以得到一个特殊解) |
| 左零空间 | $m-r$ | 对$A$进行初等行变换到$R$的矩阵$E$的最后$m-r$行 |
关于行空间的一组基:
$$A=\begin{bmatrix} 1 &2 &3 &1 \\ 1 &1 &2 &1 \\ 1 &2 &3 &1\end{bmatrix} \rightarrow \begin{bmatrix} 1 &0 & 1 &1 \\ 0 &1 &1 &0 \\ 0 &0 &0 &0\end{bmatrix}$$
因为在化成最简行阶梯形式$R$的过程中经历了行变化,此时$C(A)\neq C(R)$,但是他们的行空间却是相等的,所以行空间的一组基就是最简行阶梯形式$R$的前r行
关于左零空间:
$A^{T}y=0$,$y$就在$A$转置矩阵的零空间中
对两边进行转置,可得:$y^{T}A=0$,这个时候$y_{T}$对$A$进行左乘,所以得名左零空间
使用高斯-若当法(就是之前求逆的那个方法),来求左零空间
$$ E\begin{bmatrix} A_{m\times n}| I_{m\times m}\end{bmatrix} \rightarrow \begin{bmatrix} R_{m\times n} | E_{m\times m}\end{bmatrix} $$
因为最简行阶梯矩阵$R$的形式是酱紫的:
$$E_{m\times m}A_{m\times n}=R_{m\times n}=\begin{bmatrix} \colorbox{yellow}{I} \colorbox{pink}{F} \\ \colorbox{orange}{0\quad 0} \end{bmatrix}$$
$R$的下面$m-r$行都是0,所以对应于$E_{m\times m}$的最后$m-r$行就是左零空间的基
左乘是行变换(左行右列),$E_{m\times m}$最后几行,左乘$A$得到的行都是0,所以是左零空间的基
11. 矩阵空间和秩1矩阵
矩阵空间
把矩阵当做向量,满足加法和数乘
这里讨论所有的3x3矩阵组成的空间$M$
对于$M$,他的一组基是
$$ \begin{bmatrix} 1 &0 &0 \\ 0 &0 &0 \\ 0 &0 &0 \end{bmatrix} \begin{bmatrix} 0 &1 &0 \\ 0 &0 &0 \\ 0 &0 &0 \end{bmatrix} \cdots \begin{bmatrix} 0 &0 &0 \\ 0 &0 &0 \\ 0 &0 &1 \end{bmatrix} $$
所以$M$的维度是9,(维度的定义即需要至少九组线性无关的基来生成整个空间)
$M$的子空间:所有的上三角矩阵、对称矩阵、对角矩阵,….
| 维度 | ||
|---|---|---|
| 对称矩阵$S$ | 6 | 对称矩阵不是对角矩阵 |
| 上三角矩阵$U$ | 6 | |
| 对角矩阵$D$ | 3 |
秩1矩阵
所有的秩1矩阵都可以写成䘝列向量乘以一个行向量的形式,即$A=uv^{T}$
$$A = \begin{bmatrix} 1 &4 &5 \\ 2 &8 &10 \end{bmatrix}=\begin{bmatrix} 1 \\2\end{bmatrix}\begin{bmatrix} 1 &4 &5\end{bmatrix}$$
通过秩1矩阵,可以搭建出来任何矩阵,比如秩4矩阵通过4个秩1矩阵进行线性组合就可以搭建出来
举个例子:
$S$表示所有4维空间中的向量$v=\begin{bmatrix} v_{1}\\v_{2}\\v_{3}\\v_{4} \end{bmatrix}\in \mathbb{R}^{4}$,并且满足$v_{1}+v_{2}+v_{3}+v_{4}=0$
首先$S$是$\mathbb{R}^{4}$中的一个子空间,因为向量$v$满足加法和数乘的封闭
其次,$S$空间的基向量和维数:
令$Av=0$,可得到一个符合条件的矩阵$A=\begin{bmatrix} 1 &1 &1 &1\end{bmatrix}$,那么$S=N(A)$,$S$其实就是$A$的零空间,所以他的维数是3
同理,$S$的一组基是
$$ \begin{bmatrix} -1 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} -1 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \quad \begin{bmatrix} -1 \\ 0 \\ 0 \\ 1 \end{bmatrix} $$
矩阵$A$的列空间是$\mathbb{R}^{1}$,矩阵$A$的转置零空间$N(A^{T})$是零维的,这个子空间只有一个空集,没有基
12. 线性代数的应用:图和网络
14. 正交向量与正交子空间
正交向量(orthogonal vectors): 在n为空间中,这些向量的夹角是90° (垂直的另一种说法)。即 $x^{T}y=0$
简单的一种证明(从直角公式开始推):
$$||x||^{2}+||y||^{2} = ||x+y||^{2}$$
$$\begin{array}{c} x^{T}x+y^{T}y&=(x+y)^{T}(x+y) \\\\ &\quad =x^{T}x+y^{T}y + 2x^{T}y \end{array}$$
正交子空间(orthogonal subspace): 子空间$S$和子空间$T$正交,表示$S$中的每个向量都和$T$中的每个向量正交
行空间正交于零空间 $\because Ax=0$,$x$与$A$中的所有行都正交,同时垂直于他们的线性组合(即行空间)
他们两个是$\mathbb{R}^{n}$空间的正交补(orthogonal complements) [补集]
同理,列空间正交于左零空间
如何求一个误解方程组的解,即当 $Ax=b$ 无解的时候,如何去解这个方程组(特别是$m>n$情况下):最小二乘法
对矩阵$A_{m \times n}$来说,一个特别好的矩阵: $A^{T}A$
- $A^{T}A$是$n\times n$的方阵
- $A^{T}A$是对称阵
- $N(A^{T}A) = N(A)$, $rank(A^{T}A)=rank(A)$,所以$A^{T}A$可逆当且仅当$A$的各列线性无关,零空间只有一个零向量
$Ax=A^{T}b$ 无解时, 可以通过 $A^{T}A\hat{x}=A^{T}b$ 求最优解, 但是 $A^{T}A\hat{x}=A^{T}b$ 和 $Ax=A^{T}b$ 的解是不一样的,所以加个小帽子以区分
15. 子空间投影
一维空间
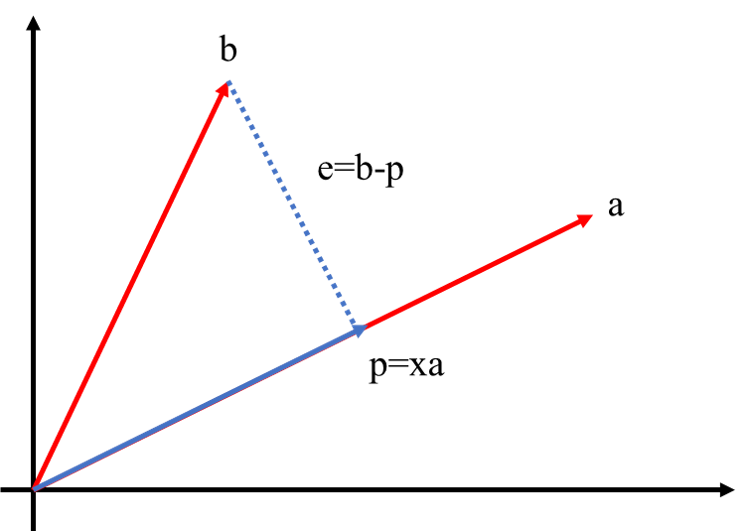
$a$ 是一维空间,想要了解到在空间$a$上离向量$b$最近的一点
$a$ 上离 $b$ 最近的一点是 $p$,$p$ 和 $b$ 正交,$p$ 和 $b$ 之间的误差是 $e=b-p$
投影 $p$ 在空间 $a$ 上,是 $a$ 的 $x$ 倍 ($x$是一个标量,而$a$和$b$是向量),所以关键就是怎么求 $x$
$$a^{T}(b-xa) = 0$$
$$\therefore x=\frac{a^{T}b}{a^{T}a}$$
最终,$b$ 在 $a$ 上的 投影 就是
$$p=a\frac{a^{T}b}{a^{T}a}$$
由上式可知,投影是通过一个 投影矩阵(projection matrix) $P$ 完成的:
$$p=Pb, \qquad P_{n\times n} = \frac{aa^{T}}{a^{T}a}$$
下面主要来分析投影矩阵的一些性质:
- 投影矩阵的列空间 $C(P)$ 是通过 $a$ 的一条线,$rank(P)=1$
- 这个矩阵是对称的 $P^{T}=P$
- 投影矩阵的平方还是自己 $P^{2}=P$, (相当于投影两次)
高维空间
为什么需要投影?
$Ax=b$可能会误解,只能求解最接近这个解的解,所以通过投影来微调$b$,即 $A\hat{x}=p$, $p$ 是 $b$ 在列空间上的投影
$A\hat{x} = p = A(A^{T}A)^{-1} A^{T} b$
$\therefore A^{T}A\hat{x} = A^{T}b$
现在有一个向量 $b$ 想要投影到 $A$ 的列空间上,得到投影向量 $p$
令 $A$ 的列空间中两个基向量为 $a_{1}, a_{2}$
那么投影向量的表达为: $p = \hat{x_{1}}a_{1} + \hat{x_{2}}a_{2} = A\hat{x}$
同一维中的推理,需要通过垂直来辅助:
$$e = (b-p) = (b-A\hat{x}) \quad \bot \quad C(A)$$
$$ \therefore \begin{cases} a_{1}^{T}(b-A\hat{x}) = 0 \\ a_{2}^{T}(b-A\hat{x}) = 0 \end{cases} $$
$$\therefore A^{T}(b-A\hat{x})=0$$
$e$ 在 $N(A^{T})$ 的空间中,即 $e\bot C(A)$,殊途同归。最终希望得到的 $\hat{x}$ 如下表达:
$$A^{T}A\hat{x} = A^{T}b$$
下面就是最重要的投影三个公式:
系数 $\hat{x}$:
$$\hat{x} = (A^{T}A)^{-1} A^{T} b$$
投影 $p$:
$$p=A\hat{x}=A(A^{T}A)^{-1} A^{T} b$$
投影矩阵 $P$:
$$P = A(A^{T}A)^{-1} A^{T}$$
如果 $A$ 是一个可逆的方阵,那么他的列空间是整个$n$维空间,那么 $P=I$,相当于我投我自己,就没有用,所以上面是唯一一种形式
同一维情况一样
- 这个矩阵是对称的 $P^{T}=P$
- 投影矩阵的平方还是自己 $P^{2}=P$
16. 投影矩阵和最小二乘
投影矩阵
如果 $b$ 在列空间 $C(A)$ 中,$Pb = b$
如果 $b$ 垂直于列空间 $C(A)$ 中,$Pb = 0$
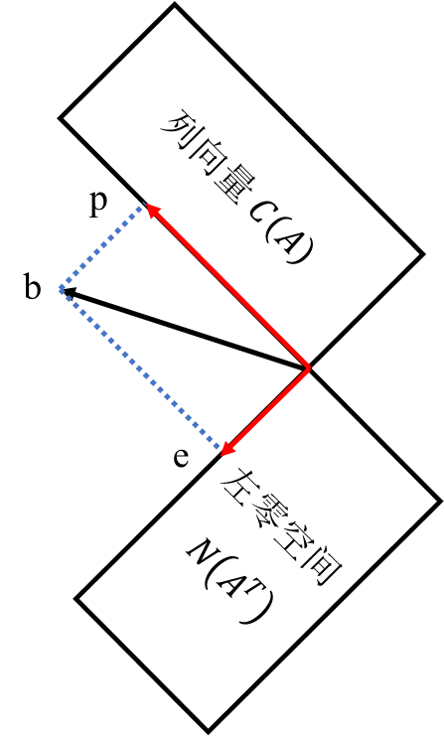
在几何上表示:列空间垂直于左零空间。对于一个典型的$b$,投影到列空间得到$p=Pb$
投影部分和误差部分加起来其实就是向量 $b$ ,即 $p+e = b$
而误差部分 $e=b-p=b-Pb = b(I-P)$ 其实相当于 $b$ 在左零空间上的投影
因为投影不管投影多少次都不会在变,所以平方的性质仍然存在 $(I-P)^{2} = (I-P)$
最小二乘法
举个例子:$(1,1); (2,2); (3,2)$ 拟合出来一条直线
设最优的直线是 $b = C+Dt$,需要确定 $C$ 和 $D$ 的参数。
带入上面三个点的参数,得到方程:
$$ \begin{cases} C + D = 1 \\ C + 2D = 2 \\ C + 3D = 2 \\ \end{cases} $$
$$ \begin{bmatrix} 1 &1 \\ 1 &2 \\ 1 &3 \end{bmatrix} \begin{bmatrix} C \\ D \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3\end{bmatrix} \rightarrow Ax = b$$
这个方程是无解的,但是他可以有最优解,最优意味着最小化他的误差
$$\min{||e||^{2}}\rightarrow \min{||Ax-b||^{2}} = \min{(e_{1}^{2}+e_{2}^{2}+e_{3}^{2})}$$
$$\min{[(C+D-1)^{2}+(C+2D-2)^{2}+(c+3D-2)^{2}]}$$
所以可以通过对$C$和$D$求偏导进行求最优解
但是使用投影的方法可以利用线性方程组很快
$$\begin{bmatrix} 1 &1 &1 \\ 1 &2 &3 \end{bmatrix} \left[\begin{array}{cc|c} 1 &1 &1 \\ 1 &2 &2 \\ 1 &3 &2 \end{array}\right] = \left[\begin{array}{cc|c} 3 &6 &5 \\ 6 &14 &11 \end{array}\right]$$
这里还有一个小技巧,就是求解$A^{T}Ax=A^{T}b$的时候可以直接对$A^{T}[A|b]$进行计算
$$ \begin{cases} 3C + 6D = 5 \\ 6C + 14D = 11 \end{cases} $$
下面对于最小二乘法只有一个难题,就是需要证明$A$是线性无关的时候,$A^{T}A$是可逆的
即$A^{T}Ax=0$只有一个零解
两边都点乘$x^{T}$,得到 $x^{T}A^{T}Ax=0$
$$(Ax)^{T}(Ax)=0 \Rightarrow Ax=0$$
$x^{T}x$ 转置乘本身相当于求$x$的长度的平方
因为$A$线性无关,所以$Ax=0$只有一个零解
17. 正交基和正交矩阵
标准正交基
一组标准正交基(orthonormal vector): $q_{1},q_{2},\cdots,q_{n}$,任意的$q$都和其他$q$正交,并且因为是“标准”的,所以他们的长度是1,即满足下面的条件
$$ q_{i}^{T}q_{j} = \begin{cases} 1, \text{if } i = j \\ 0, \text{if } i \quad!= j \end{cases} $$
上面的不等号渲染有问题,所以使用!=代替了
标准正交矩阵
标准正交矩阵(方阵): $Q=\begin{bmatrix} q_{1},q_{2},\cdots,q_{n}\end{bmatrix}$
下面研究一下标准正交矩阵的性质:
$$ Q^{T}Q = \begin{bmatrix} q_{1}^{T} \\ q_{2}^{T} \\ \vdots \\ q_{n}^{T} \end{bmatrix} \begin{bmatrix} q_{1} &q_{2} & \vdots & q_{n} \end{bmatrix}= \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{bmatrix} = I$$
即:$Q^{T} = Q^{-1}$,但是$Q$必须是方阵
对于投影矩阵$P$,他是 $P^{T} = P$
对标准正交基举个例子:
$$ \frac{1}{2} \begin{bmatrix} 1 &1 &1 &1 \\ 1 &-1 &1 &-1 \\ 1 &1 &-1 &-1 \\ 1 &-1 &-1 &1 \\ \end{bmatrix}$$
举几个标准正交基的好处:
投影
$Q$是标准正交基,现在要将向量投影到他的列空间中,投影矩阵:
$$P = Q(Q^{T}Q)^{-1}Q^{T}= QQ^{T}$$
当$Q$是方阵时,$Q$的列空间就是整个空间,所以投影矩阵是$I$;如果不是方阵,那么结果就是上述这个
最小二乘法
$$A^{T}A\hat{x} = A^{T}b \rightarrow Q^{T}Q\hat{x} = Q^{T}b \rightarrow \hat{x} = Q^{T}b$$
线性无关向量标准正交化
格拉姆-施密特正交化法 (Gram-Schmidt)
其实就是逐个向量减去之前向量的分量(即之前向量在这个向量空间上的投影)
对于两个向量 $a$ 和 $b$,标准正交化的向量 $q_{1}$ 和 $q_{2}$
$$a’ = a;\qquad b’=b-Pa’=b-\frac{a’^{T}b}{a’^{T}a’}a’$$
$$q_{1} = \frac{a’}{||a’||};\qquad q_{2} = \frac{b’}{||b’||}$$
下面验证一下分量$a’$和$b’$正交
$$a’^{T}b’ = a’^{T}(b-\frac{a’^{T}b}{a’^{T}a’}a’) = 0$$
所有,以后对于列空间的基,可以有了性质更好的描述,就是标准正交基
重新用矩阵的角度审视消元法:
$$A=LU \rightarrow A=Q^{T}R=QR$$
$$ \begin{bmatrix} a &b \end{bmatrix} = \begin{bmatrix} q_{1} &q_{2} \end{bmatrix} \begin{bmatrix} a_{1}^{T}q_{1} &\cdots \\ a_{1}^{T}q_{2} &\cdots \end{bmatrix} $$
因为 $R$ 与 $A$ 的列空间一致,所以可以表达为每个分量
$$ A = \left[\begin{array}{lll} a & b & c \end{array}\right]=\left[\begin{array}{lll} q_{1} & q_{2} & q_{3} \end{array}\right]\left[\begin{array}{lll} q_{1}^{T} a & q_{1}^{T} b & q_{1}^{T} c \\\\ & q_{2}^{T} b & q_{2}^{T} c \\\\ & & q_{3}^{T} c \end{array}\right] = QR$$
这个其实就相当于了格拉姆-施密特的正交过程了
而 $R$ 为什么是上三角矩阵,因为每一个后面的 $q$ 都要与前面的列向量正交
18. 行列式及其性质
接下来把重点放到了方阵上,行列式的目的是为了矩阵的特征值
矩阵的 行列式(determinant) 记作 $\det{A}$ 或者 $|A|$
行列式的三个性质定义了行列式是个什么东西:
- $\det{I} = 1$,使得单位矩阵的行列式为1,(定义基准)
- 交换行,行列式的值的符号会相反,(现在知道了置换矩阵的行列式)
- 行列式是一个线性函数,对每一行都成立
$$\begin{vmatrix} ta &tb \\ c &d \end{vmatrix}= t \begin{vmatrix} a &b \\ c &d \end{vmatrix}$$
$$\begin{vmatrix} a+a’ &b+b’ \\ c &d \end{vmatrix}= \begin{vmatrix} a &b \\ c &d \end{vmatrix}+\begin{vmatrix} a’ &b’ \\ c &d \end{vmatrix}$$
由上面三个性质可以继续推导出下面的性质来:
两行相等使得行列式等于0 (可以由性质2得到)
从行$k$减去行1的$i$倍,行列式不变(性质3+性质2)
若有一行为0,那么行列式就是0 (性质3,$t=0$)
上三角矩阵的行列式等于对角线元素的乘积
$$\det{U}=\begin{vmatrix} d_{1} & \cdots & \cdots & \cdots \\ & d_{2} & \cdots & \cdots \\ & & \ddots & \vdots \\ \Huge0 & & &d_{n} \\ \end{vmatrix}=d_{1}d_{2}\cdots d_{n}$$因为上三角矩阵$U$和原矩阵$A$之间只经过了性质6的线性变换,所以原矩阵$A$的行列式就等于上三角矩阵$U$的行列式
如果其中一个对角线元素为0,那么将得到全0行,行列式为0
$\det{A}=0$ 当且仅当 $A$ 是奇异矩阵,(不可逆)
两个方阵$A$和$B$的矩阵乘积的行列式等于他们行列式的乘积 $\det{AB}=\det{A}\times\det{B}$。所以可以推导出下面:
$$\det{A^{-1}} = \frac{1}{\det{A}}$$
这个其实也说明,如果没有逆,$det{A}=0$,逆就没有意义
$$\det{A^{2}} = (\det{A})^{2}$$
$$\det{2A} = \det{2I}\det{A} = 2^{n}\det{A}$$
矩阵的行列式等于矩阵转置的行列式
$$\det{A^{T}}=\det{A}$$
从这里其实就可以发现,对于行列式来说,行和列并没有什么区别,都是进行行变换/列变换要改变符号的
简单的证明一下:要证 $|A^{T}|=|A|\rightarrow |U^{T}L^{T}|=|LU|$
$L$是一个下三角阵,并且对角线上全是1,所以$|L|=1$,同理,转置后的$L$对角线上也全是1,所以 $|U^{T}|=|U|$
19. 行列式公式和代数余子式
有了以上的性质,特别是性质7之后,可以给探究一下行列式的定义,即通过消元法来求行列式的值
首先对于2阶矩阵:
$$ \begin{bmatrix} a &b \\ c &d \end{bmatrix} \rightarrow \begin{bmatrix} a &b \\ 0 & d-\frac{c}{a}b \end{bmatrix} \rightarrow \det = a(d-\frac{c}{a}b) = ad-bc$$
对于3阶矩阵的行列式:
使用性质三,对一个三阶行列式进行分解:因为如果其中一行/列全是0则行列式等于0,所以分解结果得到的是6个有值的行列式
$$ \begin{aligned} \left|\begin{aligned} & a_{11} & a_{12} && a_{13} \\ & a_{21} & a_{22} && a_{23} \\ & a_{31} & a_{32} && a_{33} \\ \end{aligned}\right| &= \left|\begin{aligned} & a_{11} & 0 && 0 \\ & 0 & a_{22} && 0 \\ & 0 & 0 && a_{33} \\ \end{aligned}\right| + \left|\begin{aligned} & a_{11} & 0 && 0 \\ & 0 & 0 && a_{23} \\ & 0 & a_{33} && 0 \\ \end{aligned}\right| + \left|\begin{aligned} & 0 & a_{12} && 0 \\ & a_{21} & 0 && 0 \\ & 0 & 0 && a_{33} \\ \end{aligned}\right| \\ &+ \left|\begin{aligned} & 0 & a_{12} && 0 \\ & 0 & 0 && a_{23} \\ & a_{31} & 0 && 0 \\ \end{aligned}\right| + \left|\begin{aligned} & 0 & 0 && a_{13} \\ & a_{21} & 0 && 0 \\ & 0 & a_{32} && 0 \\ \end{aligned}\right| + \left|\begin{aligned} & 0 & 0 && a_{13} \\ & 0 & a_{22} && 0 \\ & a_{31} & 0 && 0 \\ \end{aligned}\right| \\ &=a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \\ &+a_{12}a_{23}a_{32} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} \end{aligned} $$
而在这里其实就能发现:
对于$n$阶矩阵($n\times n$),他的行列式表达式中有 $n!$ 项,因为可以看出,如果其中一行/列全是0则行列式等于0,那么就是排列问题了,第一行有$n$中选择,第二行有$n-1$种可能,以此类推
所以$n$阶行列式的形式应该是这种形式的:
$$\det{A} = \sum{\pm a_{1\alpha}a_{2\beta}\cdots a_{n\gamma}}$$
$a_{ij}$表达了$i$行$j$列的元素,那么$\alpha,\beta,\cdots,\gamma$其实就是$(1,2,\cdots,n)$的一种排列
而前面的正负号其实取决于$(\alpha,\beta,\cdots,\gamma)\rightarrow (1,2,\cdots,n)$这两种排列需要进行变换的奇偶次数
将上面的进行凝练,通过代数余子式来说明行列式的求解:
代数余子式 (cofactors)
首先还是考虑简单的三阶情况:
$$ \begin{aligned} \det & = a_{11}(a_{22}a_{33}-a_{23}a_{32}) \\ & + a_{12}(\cdots) \\ & + a_{13}(\cdots) \end{aligned} $$
可以将行列式表达换成上面的这种形式,选定第一行中的一个数,然后由剩余因子组成的表达式就是代数余子式,即以$a_{11}$括号内的$(a_{22}a_{33}-a_{23}a_{32})$就是$a_{11}$的代数余子式
$$\text{Cofactor}(a_{ij})=(-1)^{ij}\det(n-1\quad \text{matrix with}\begin{aligned}row_{i} \\ col_{j}\end{aligned} \text{earsed})$$
通过代数余子式,就可以进行扩展到n阶行列式的计算:
$$det\space A = \sum_{i}^{n}a_{1i}C_{1i}$$
20. 行列式的应用:逆矩阵、克拉默法则、体积
行列式引出的目的就是为了求解特征值,但是这不妨碍他还有一些其他的应用
逆矩阵
因为行列式关于矩阵逆的独特性质 $\det{A^{-1}} = \frac{1}{\det{A}}$
首先还是考虑 $2\times2$ 的逆矩阵情况:
$$ \begin{bmatrix} a &b \\ c &d \end{bmatrix}^{-1}= \frac{1}{ad-bc} \begin{bmatrix} d &b \\ -c &a \end{bmatrix} $$
可以看到,归一化的 $\frac{1}{ad-bc}=\det(A)$
右边的矩阵就是各个位置对应的代数余子式,即
$$A^{-1}=\frac{1}{\det(A)}C^{T}$$
其中,$C$是由代数余子式构成的矩阵,$C^{T}$一般称为伴随矩阵
下面简单证明一下:
$$ \begin{aligned} & A^{-1}=\frac{1}{det(A)}C^{T} \Rightarrow AC^{T}=det(A)I \\ & A=\begin{bmatrix} \color{blue}a_{11} & \color{blue}a_{12} & \color{blue}\cdots & \color{blue}a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} C^{T}=\begin{bmatrix} \color{blue}c_{11} & c_{21} & \cdots & c_{n1} \\ \color{blue}c_{12} & c_{22} & \cdots & c_{n2} \\ \color{blue}\vdots & \vdots & \ddots & \vdots \\ \color{blue}c_{1n} & c_{2n} & \cdots & c_{nn} \\ \end{bmatrix} \end{aligned} $$
$AC^{T}$在对角线上的每一个值正好都是行列式的代数余子式表达,如果不在对角线,把他还原成对应矩阵,会有相同的两行,即奇异矩阵,$\det=0$
$$ AC^{T}= \begin{bmatrix} detA & & & \Huge0 \\ & detA & & \\ & & \ddots & \\ \Huge0 & & & detA \end{bmatrix} =det(A)\cdot I $$
克拉默法则
提供一种代数形式的表达,但不适合计算
求解:$Ax=b$
$$x=A^{-1}b=\frac{1}{\det{A}}C^{T}b$$
其中,$x_{j}=\frac{det(B_{j})}{det(A)}$,$B_{j}$是$A$的第$j$列替换成$b$
举个例子:
$$ B_{1} =\begin{bmatrix} b_{1} & a_{12} & \cdots & a_{1n} \\ b_{2} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} $$
即矩阵$A$的第$j$列用$b$来代替$\Rightarrow$克拉默法则
计算体积
还是先从简单的来说,比如 $3\times 3$的情况:
有3个向量:$(a_{11}, a_{12}, a_{13}); (a_{21}, a_{22}, a_{23}); (a_{31}, a_{32}, a_{33})$他们在空间中组成了一个“箱子”
这个箱子的体积就等于这几个向量构成的矩阵的行列式的绝对值,即 $|\det A|$
首先考虑最基本的情况:对于标准正交矩阵 $Q$,证明他的“箱子”的体积是1
$$ Q^{T}Q = I \rightarrow \det{Q^{T}}\det{Q} = \det{I} = 1 \rightarrow (\det{Q})^{2} =1 \rightarrow \det{Q}=1$$
在这个基础上,拓展成长方块也同样成立,接下来就是证明对于任意角度的向量都可以 [通过行列式的线性性质进行计算,也就是把平行四边形拆成一个长方形进行计算]
21. 特征值和特征向量
特征值和特征向量还是针对方阵而言的
给定矩阵$A$,作用在向量$x$,($A$就像是一个函数对$x$进行变换然后得到了一个新的向量),得到的新的向量$Ax$与原向量$x$平行,即
$$Ax=\lambda x$$
其中,$\lambda$是一个系数,称为特征值(eigen value),$x$是特征向量(eigen vector)
首先还是来看两个例子
投影矩阵的特征值和特征向量
当$x$在平面上时(即投影矩阵$P=A(A^{T}A)^{-1}A^{T}$所要投影到的$A$的列空间上,即$C(A)$),$Px=x$,所以特征值为$\lambda=1$
当$x$垂直于平面是,$Px=0$,所以特征值为$\lambda=0$
所以我们可以知道投影矩阵$P$的两个特征值,分别是$\lambda=0,1$
置换矩阵的特征值和特征向量
这里使用$A=\begin{bmatrix} 0 &1 \\ 1 &0\end{bmatrix}$来表示置换向量,避免与上面的投影矩阵$P$混淆
他的一组特征向量和特征值可以是$x=\begin{bmatrix} 1 \\ 1\end{bmatrix}, \lambda = 1$;另一组可以是$x=\begin{bmatrix} -1 \\ 1\end{bmatrix}, \lambda = -1$
如何求解特征值和特征向量,即$Ax=\lambda x$
将上式重写成: $(A-\lambda I)x=0$,即如果存在$x$使得这个式子成立,那么$A$进行$\lambda I$的偏移后必须是奇异的
奇异矩阵的行列式为0,所以 $\det(A-\lambda I)=0$,这个方程被称为特征方程/特征值方程
举个例子:$A=\left|\begin{aligned}&3&1 \\ &1&3\end{aligned}\right|$
$\therefore \det(A-\lambda I)=\left|\begin{aligned} &3-\lambda & 1 \\ &1 &3-\lambda \end{aligned}\right|=(3-\lambda)^{2}-1=\lambda^{2}-\color{blue}{6}\color{red}\lambda+\color{green}8$
这里的 $\color{blue}{6}$ 是矩阵$A$的迹, $\color{green}{8}$ 是矩阵A的行列式值,对于二阶行列式有这个性质
$\therefore$ 有两个特征值:$\lambda_{1}=4$ $\lambda_{2}=2$
$\lambda_{1}=4$时,$(A-\lambda I)=\begin{bmatrix}-1 &1 \\ 1 &-1\end{bmatrix}$, $x_{1}=\begin{bmatrix}1 \\1\end{bmatrix}$
$\lambda_{2}=2$时,$(A-\lambda I)=\begin{bmatrix}1 &1 \\ 1 &1\end{bmatrix}$, $x_{2}=\begin{bmatrix}-1 \\1\end{bmatrix}$
还有另一个例子:$A=\left|\begin{aligned}&1&0 \\ &0&1\end{aligned}\right|$
得到他的两组特征值和特征向量是:
$\lambda_{1}=1$时, $x_{1}=\begin{bmatrix}1 \\1\end{bmatrix}$
$\lambda_{2}=-1$时, $x_{2}=\begin{bmatrix}-1 \\1\end{bmatrix}$
从这两个例子看出来,第一个例子的矩阵成为$A_{1}$,第二个例子的矩阵称为$A_{2}$,
$A_{1} = A_{2} + 3I$。对于特征值来说其实就是相应的+3,对于特征向量来说其实不变。
所以特征值和特征向量反应了一个矩阵的另一个属性。
特征值\特征向量比较糟糕的情况
1. 出现复数
记旋转矩阵$Q$为使矩阵中每个向量旋转90°的矩阵,二维即:
$$Q=\begin{bmatrix} \cos{90^{\circ}} & -\sin{90^{\circ}}\\ \sin{90^{\circ}} & \cos{90^{\circ}} \end{bmatrix} =\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$$
通过刚才可以知道:
$$ \begin{cases} \text{trace} = 0+0 = \lambda_{1} + \lambda_{2} \\ \det = 1 = \lambda_{1}\lambda_{2} \end{cases} $$
$\lambda_{1}$和$\lambda_{2}$没有实数解,有复数解:$\lambda_{1}=i$ 和 $\lambda_{2}=-i$
解释其实就是,对向量旋转90°,除非是零向量,否则不可能出现$Ax=\lambda x$中平行的情况
2. 出现重根
上三角矩阵: $A=\begin{bmatrix} 3 &1 \\ 0&3\end{bmatrix}$
顺带一提,上三角矩阵的特征值就是对角线上的元素
他的两个特征值都是: $\lambda_{1} = \lambda_{2} = 3$
所以这个矩阵的特征向量是:
$$ (A-\lambda I)x = \begin{bmatrix} 0 &1 \\ 0 &0 \end{bmatrix}x = 0 \rightarrow x_{1} = \begin{bmatrix} 1 \\ 0\end{bmatrix} $$
只有一个特征向量,没有第二个无关的特征向量
特征值的性质:
- 特征值的和($\sum\lambda$)等于矩阵A对角线元素之和,即迹(trace):$a_{11}+…+a_{nn}$
22. 对角化和幂
特征向量矩阵$S$:将矩阵$A$的n个线性无关的特征向量按列组成的矩阵(即可逆)
特征值矩阵$\Lambda$:矩阵$A$的n个特征值构成的矩阵,特征值在矩阵的对角线上
$$S^{-1}AS = \Lambda$$
$$AS=S\Lambda$$
$$A=S\Lambda S^{-1}$$
对上式进行一个推导:
$$ \begin{aligned} AS & = A\begin{bmatrix} x_{1} &x_{2} & \cdots &x_{n}\end{bmatrix} \\ & = \begin{bmatrix}\lambda_{1}x_{1} &\lambda_{2}x_{2} &\cdots &\lambda_{n}x_{n}\end{bmatrix} \\ & = \begin{bmatrix} x_{1} &x_{2} & \cdots &x_{n}\end{bmatrix}\begin{bmatrix} \lambda_{1} &0 &\cdots &0 \\ 0 &\lambda_{2} &\cdots &0 \\ \vdots &\vdots &\ddots &\vdots \\ 0 &0 &\cdots &\lambda_{n} \end{bmatrix} \end{aligned} =S\Lambda $$
这个就是矩阵的对角化方法,最后得到矩阵$\Lambda$
$$A=S\Lambda S^{-1}$$
一种新的矩阵分解,可以拓展原来的思考,比如计算矩阵的平方$A^{2}$:
$$Ax = \lambda x \rightarrow A^{2}x = \lambda Ax = \lambda^{2}x$$
$$A^{2} = S\Lambda S^{-1}S\Lambda S^{-1} = S\Lambda^{2}S^{-1}$$
上面两个式子说明了同一件事:$A^{2}$的特征值是$A$的平方,$A$的特征向量和$A^{2}$一样,对角化提供了一种以矩阵形式思考的解决方法。
同理,可拓展到$K$次幂:
$$A^{k} = S\Lambda^{k}S^{-1}$$
但是对于$A=LU$分解这是不可用的
进行对角化的条件:
矩阵$A$没有重复的特征值(充分不必要)。如果存在重复的特征值,可能但不一定存在n个线性无关特征向量(比如n维的单位向量,特征值只有1,但是特征向量是每一列),只要没有重复的特征向量就行。
求解差分方程:
$$ \begin{cases} \text{初始向量 } u_{0} \\ \text{差分方程 } u_{k+1} = Au_{k} \end{cases} $$
$$u_{k} = A^{k}u_{0}$$
其中,初始矩阵$u_{0}$可以写成$A$的特征向量的线性组合形式 (因为特征向量之间线性无关,$A$非奇异不会产生重复的特征向量看,所以特征向量矩阵的列空间铺满了整个空间)
$$u_{0} = c_{1}x_{1} + c_{2}x_{2} + \cdots + c_{n}x_{n}$$
$$Au_{0} = c_{1}\lambda_{1} x_{1} + c_{2}\lambda_{2}x_{2} + \cdots + c_{n}\lambda_{n}x_{n}$$
$$A^{100}u_{0} = c_{1}\lambda_{1}^{100} x_{1} + c_{2}\lambda_{2}^{100}x_{2} + \cdots + c_{n}\lambda_{n}^{100}x_{n}$$
举个例子:斐波那契数列
$$F_{k+2}=F_{k+1}+F_{k}\qquad [0, 1, 1, 2, 3, 5, 8, 13, 21, …]$$
定义向量:$u_{k}=\begin{bmatrix}F_{k+1}\\F_{k}\end{bmatrix}\therefore\left\{\begin{aligned} &F_{k+2} = F_{k+1} + F_{k} \\ &F_{k+1} = F_{k+1} \end{aligned}\right.\Rightarrow u_{k+1}=Au_{k};A=\begin{bmatrix} 1 &1 \ 1 &0 \end{bmatrix}$
A的特征值:$\lambda=\frac{1\pm \sqrt{5}}{2}$
因为斐波那契数列是增长的,所以增长速度应该是 $\lambda_{1}=\frac{1+\sqrt{5}}{2}$
从$u_{0}=\begin{bmatrix}F_{1}\\F_{0}\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}=c_{1}x_{1}+c_{2}x_{2}$ 可以求得 $c_{1}=\frac{1}{\sqrt{5}}$,$c_{2}=-\frac{1}{\sqrt{5}}$
所以,$\begin{bmatrix}F_{100}\\F_{99}\end{bmatrix}=A^{99}\begin{bmatrix}F_{1}\\F_{0}\end{bmatrix}$,$F_{100}=c_{1}\lambda_{1}^{100}+c_{2}\lambda_{2}^{100}$
所以,$F_{100}\approx c_{1}\lambda_{1}^{100}$
23. 微分方程和exp(At)
这一部分看不太懂,看常微分方程的时候再回过头来看
24. 马尔科夫矩阵和傅里叶级数
特征值和特征矩阵的应用
马尔科夫矩阵
马尔科夫矩阵,满足两条性质:1. 每个元素大于等于0; 2. 每一列相加都等于0 (与概率有着非常紧密的联系)
假设使用马尔科夫矩连续乘以一个正的向量$u_{0}$,即
$$u_{1} = Au_{0}; \qquad u_{2} = Au_{1}; \quad \cdots;\quad u_{n} = Au_{n-1}$$
k步之后我们可以得到$A^{k}u$,这些向量会最终接近一个稳定状态,比如:
$$A=\begin{bmatrix} .8 & .3 \\ .2 & .7\end{bmatrix}$$
对于每一个$u_{0}=(a,1-a)$,都可以收敛到稳定的状态:$u_{\infty}=(0.6,0.4)$
现在来讨论能到达稳态的条件:
- $\lambda=1$是马尔科夫矩阵$A$的特征值
- 马尔科夫矩阵$A$的其他特征值都绝对值小于1,即 $|\lambda|<1$
在遇到矩阵连乘时,根据特征值分解,我们可以得到:
$$u_{k} = A^{k}u_{0} = u_{0}(c_{1}\lambda_{1}^{k} x_{1} + c_{2}\lambda_{2}^{k}x_{2} + \cdots + c_{n}\lambda_{n}^{k}x_{n})$$
所以,要想$u_{\infty}$到达稳态,必须有一个特征值为1,其他特征值项逐渐消失才行
现在要判断马尔科夫矩阵一定有一个特征值等于一,所以判断$A-I$是不是奇异的:
当$A-I$所有列相加得到0,就说明$A-I$是奇异的
因为马尔科夫矩阵每一列和为1,所以$A-I$每一列和为0,所以用行向量$(1,1,1)$左乘$A-I$可以得到0,即$(0,0,0)A=0$,说明(1,1,1)在$A-I$的左零空间中,行向量线性相关,矩阵是奇异的
这里其实就拓展出来好多,因为对于行列式来说行列是无关的$\det(A)=\det(A^{T})$,而只要 $\det=0$ 矩阵就奇异,所以只要零空间/左零空间有非0向量,那么这个矩阵就是奇异的
还有特征值的一个性质:矩阵和其转置的特征值是一样的
证明:$\det(A-\lambda I)=0 \rightarrow \det(A^{T}-\lambda I)=0$
傅里叶级数
讨论一下带有标准正交基的投影问题
给定标准正交基 $q_{1},\cdots,q_{n}$,任意向量可以以标准正交基的一个组合进行表达:
$$v=x_{1}q_{1}+x_{2}q_{2}+\cdots+x_{n}q_{n}$$
现在想要知道,对于$v$,标准正交基的组合数$x_{1},x_{2},\cdots,x_{n}$是多少
那么标准正交基在这里就非常有用了,例如想求$x_{1}$,则左右两边都对$q_{1}$做内积,因为是正交的,所以除了$x_{1}$这一项,其他都是0
$$q^{T}_{1}v=x_{1}q^{T}_{1}q_{1}+0+\cdots+0$$
因为是标准正交基,所以$q^{T}_{1}q_{1}=1$,即$x_{1}=q^{T}_{1}v$
使用矩阵形式可以得知:
$$v=Qx,\qquad Q=\begin{bmatrix} q_{1} &q_{2} &\cdots &q_{n} \end{bmatrix},\qquad x=\begin{bmatrix} x_{1} \\ \vdots \\ x_{n} \end{bmatrix}$$
可得:$x = Q^{-1}v$,因为$Q$是标准正交矩阵,所以$x=Q^{T}v$
现在代入傅里叶级数
已知函数$f(x)$,我们想把它写成组合的形式,包含常数项,也包含$\cos$,$\sin$项等,即:
$$f(x) = a_{0} + a_{1}\cos{x}+b_{1}\sin{x}+a_{2}\cos{2x}+b_{2}\sin{2x}+\cdots$$
这个就是傅里叶级数,无穷维,并且$\cos$和$\sin$还正交,它作用在函数空间上,可以用函数$f(x)$来代替$v$,可以使用正交函数$\cos,\sin,\cdots$来代替正交向量$q_{1},q_{2},\cdots$
函数的正交类比于向量的正交:
向量的正交:两个向量的点积为0,即 $v^{T}w=v_{1}w_{1}+\cdots+v_{n}w_{n}$
函数的正交:给定两个函数,记为$f$和$g$,类比于向量的正交取点积,即对于取值积$f(x)g(x)$的和为0,即 $f^{T}g=\int{f(x)g(x)}\mathrm{d}x$
现在我们关心如何求$a_{0},a_{1},\cdots$,以$a_{1}$为例,同刚才投影一样,两边对$\cos{x}$进行正交
$$\int_{0}^{2\pi}{f(x)\cos{x}\mathrm{d}x}=a_{1}\int^{2\pi}{0}(\cos{x})^{2}=\pi a{1}$$
26. 对称矩阵
对称矩阵(实数) $A=A^{T}$:
特征值是实数;
特征向量是垂直的(正交)
所以,特征值分解在对称矩阵情况下:
$$A=S\Lambda S^{-1} \rightarrow A=Q\Lambda Q^{-1}=Q\Lambda Q^{T}$$
这个等式称为“谱定理”
谱:矩阵特征值的集合
下面简要推导一下:特征值都是实数
取式子的共轭复数,同时因为指定对称矩阵是实矩阵:
$$Ax=\lambda x \rightarrow \overline{A}\overline{x} = \overline{\lambda}\overline{x} \rightarrow A\overline{x} = \overline{\lambda}\overline{x}$$
对两边取转置,右乘$x$:
$$ \overline{x}^{T}A^{T} = \overline{x}^{T}\overline{\lambda} \rightarrow \overline{x}^{T}A = \overline{x}^{T}\overline{\lambda} \rightarrow \overline{x}^{T}Ax = \overline{x}^{T}\overline{\lambda}x $$
对原矩阵两边左乘$\overline{x}^{T}$,得到:
$$\overline{x}^{T}Ax = \overline{x}^{T}\lambda x$$
结合上面两式可得:
$$\overline{x}^{T}\overline{\lambda}x = \overline{x}^{T}\lambda x$$
所以 $\lambda=\overline{\lambda}$,特征值为实数
如果是复矩阵,上述性质如实现,仍需要满足共轭条件,即$A=\overline{A}^{T}$
下面再推到一下特征向量都是正交的,即:
若$x_{1}$,$x_{2}$是对称矩阵$A$的两个特征向量,$Ax_{1}=\lambda_{1}x_{1}$,$Ax_{2}=\lambda_{2}x_{2}$,如果$\lambda_{1}!=\lambda_{2}$,则$x_{1}^{T}x_{2}=0$
令$z=x^{T}_{1}Ax_{2}$,因为$z$是标量,所以$z^{T}=z$,即
$$x_{2}^{T}A^{T}x_{1} = x^{T}{1}Ax{2}$$
因为$A$是对称的,所以有:
$$x_{2}^{T}Ax_{1} = x^{T}{1}Ax{2}$$
$$x_{2}^{T}\lambda_{1}x_{1} = x^{T}{1}\lambda{2}x_{2}$$
$$\lambda_{1}x_{2}^{T}x_{1} = \lambda_{2}x^{T}{1}x{2}$$
因为:$z^{T}=z$,所以:
$$x^{T}_{1}\lambda_{2}x_{2} = x_{2}^{T}\lambda_{2} x_{1}$$
$$\lambda_{2}x^{T}_{1}x_{2} = \lambda_{2}x_{2}^{T}x_{1}$$
结合上述两式,得到:
$$\lambda_{1}x_{2}^{T}x_{1} = \lambda_{2}x_{2}^{T}x_{1}$$
$$(\lambda_{1}-\lambda_{2})x_{2}^{T}x_{1} = 0$$
因为 $\lambda_{1}$ 不等于 $\lambda_{2}$
所以:$x_{2}^{T}x_{1} = 0$
对$A=Q\Lambda Q^{T}$继续探索:
$$ \begin{aligned} A=Q\Lambda Q^{T} &=\begin{bmatrix} q_{1} &q_{2} &\cdots\end{bmatrix} \begin{bmatrix} &\lambda_{1} && \\ &&\lambda_{2}& \\ &&&\ddots \end{bmatrix} \begin{bmatrix} q_{1}^{T} \\q_{2}^{T} \\ \vdots \end{bmatrix}\\\\ &=\lambda_{1}q_{1}q_{1}^{T}+\lambda_{2}q_{2}q_{2}^{T}+\cdots \end{aligned} $$
$q_{1}q_{1}^{T}$ 是投影矩阵,是对称的
所以每一个对称矩阵都是由一些互相垂直的投影矩阵的组合
对对称矩阵来说,主元与特征值的符号个数一致 (正主元的个数=正特征值的个数)
27. 复数矩阵和快速傅里叶变换
28. 正定矩阵和最小值
正定矩阵(postive definite matrix):所有特征值为正数的对称矩阵
对于正定矩阵的几种判定方法,以$A=\begin{bmatrix} a &b \\ c &d\end{bmatrix}$为例:
- 所有的特征值为正:$\lambda_{1}>0, \lambda_{2}>0$
- 所有主子矩阵(即西雅图子矩阵,Seattle submatrices)的行列式都是正的:$a>0, ac-b^{2}>0$
- 所有的主元都是正的: $a>0, \frac{ac-b^{2}}{a}>0$
- $x^{T}Ax>0$
举个例子:
$$A=\begin{bmatrix} 2 &6 \\ 6 &18\end{bmatrix}$$
这个是半正定矩阵,因为是奇异矩阵,所以可以得到一个特征值$\lambda_{1}=0$(所以被称为“半正定”),另一个特征值为$\lambda_{2}=20$。矩阵只有一个主元2。
对于判定方法4:
$$ \begin{bmatrix} x_{1}&x_{2}\end{bmatrix} \begin{bmatrix} 2 &6 \\ 6 &18\end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2}\end{bmatrix} =2x_{1}^{2} + 12x_{1}x_{2} + 18x_{2}^{2} $$
对于任意的$x$,如果$x^{T}Ax$总是正的,那么$A$是一个正定矩阵
但是对于这个矩阵$\begin{bmatrix} 2 &6 \\ 6 &18\end{bmatrix}$,$x^{2}Ax\ge 0$,所以他是半正定的
如果稍加修改,对矩阵$\begin{bmatrix} 2 &6 \\ 6 &7\end{bmatrix}$来说,$x^{T}Ax=2x_{1}^{2}+12x_{1}x_{2}+7x_{2}^{2}$是一个马鞍面,存在一点小于0,所以不是正定矩阵
对矩阵$\begin{bmatrix} 2 &6 \\ 6 &20\end{bmatrix}$来说,$x^{T}Ax=2x_{1}^{2}+12x_{1}x_{2}+20x_{2}^{2}>0$是一个碗面,对所有不等于0的$x$都成立。
再进一步,对得到的$x^{T}Ax$进行配方,得到$x^{T}Ax=2x_{1}^{2}+12x_{1}x_{2}+20x_{2}^{2}=2(x_{1}+3x_{2})^{2}+2x_{2}^{2}$。而矩阵进行LU分解后得到:$\begin{bmatrix} 2 &6 \\ 6 &20\end{bmatrix}=\begin{bmatrix} 1 &0 \\ 3 &1 \end{bmatrix}\begin{bmatrix} 2 &6 \\ 0 &2\end{bmatrix}$配方的本质其实就是消元,可以看到两个主元分别是两个平方的系数,$L$中的3就是配方的系数
正定可以检查函数是否存在最小值:
对于微积分来说,如果$\frac{\mathrm{d}^{2}u}{\mathrm{x}^{2}}>0$,则存在极小值
那么采用矩阵形式,则是$f(x_{1},x_{2},\cdots)$组成的矩阵是正定的
- 正定矩阵的逆也是正定的,因为特征值是原矩阵特征值的倒数,所以都是正的
- 矩阵$A, B$都是正定的, $A+B$也是正定的,因为$x^{T}(A+B)x>0$
- 对于长方矩阵$S_{m\times n}$,$S^{T}S$是正定的,$x^{T}A^{T}Ax=(Ax)^{T}Ax$,等于$Ax$的长度的平方$\ge 0$
29. 相似矩阵和若尔当形
相似矩阵:$A$和$B$是$n\times n$相似矩阵,意味着存在一个可逆矩阵$M$使得:$B=M^{-1}AM$
举个例子:特征值分解 $S^{-1}AS = \Lambda$,即$A$和$\Lambda$是相似的
相似矩阵的共同点: 他们具有相同的特征值,无关特征向量的数目也一样
简单证明一下:
$$ \begin{aligned} & Ax=\lambda x \\ & AMM^{-1}x = \lambda x \\ & M^{-1}AMM^{-1}x = \lambda M^{-1}x \\ & BM^{-1}x = \lambda M^{-1}x \end{aligned} $$
即,$\lambda$也是矩阵$B$的特征值
对于存在相等特征值的情况:
例如两个特征值相等为4: $\lambda_{1}=\lambda_{2}=4$,可以分别是如下两种矩阵:
$$ \begin{bmatrix} 4 &0 \\ 0&4\end{bmatrix},\quad \begin{bmatrix} 4 &1 \\ 0&4\end{bmatrix} $$
但是这两种情况并不一样
$\begin{bmatrix} 4 &0 \\ 0&4\end{bmatrix}$只和自己相似,$M^{-1}4IM=4I$,
$\begin{bmatrix} 4 &1 \\ 0&4\end{bmatrix}$可以代表一个大家族,称为若尔当标准型,即最简单,最接近对角阵的一个(但他不能对角化,如果能的话,他就和上面的这个矩阵相似了)
再举一个特例:
$$\begin{bmatrix} 0 &1 &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &0 \\ 0 &0 &0 &0\end{bmatrix},\quad\begin{bmatrix} 0 &1 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &0 &1 \\ 0 &0 &0 &0\end{bmatrix}$$
这两个矩阵的特征值$\lambda_{1}=\lambda_{2}=\lambda_{3}=\lambda_{4}=0$,但是很明显他们不是相似的
若尔当解释他们的分块是不一样的,第一个矩阵的分块是$\begin{bmatrix} 0 &1 &0 \\ 0 &0 &1 \\ 0 &0 &0\end{bmatrix}$和$[0]$,第二个矩阵的分块是$\begin{bmatrix} 0 &1 \\ 0 &0\end{bmatrix}$ 和$\begin{bmatrix} 0 &1 \\ 0 &0\end{bmatrix}$,所以他们是不相似的
若尔当定理: 每个方阵$A$都相似于一个若尔当阵$J$,若尔当阵即由若干个若尔当块都成的矩阵:
$$J=\begin{bmatrix} J_{1} &&& \\ &J_{2} && \\ &&\ddots& \\ &&&J_{d} \end{bmatrix}$$
若尔当块:特征值位于方阵的对角线上,若尔当块的数量等于特征向量的数量
30. 奇异值分解(SVD)
矩阵最终和最好的分解
$$A=U\Sigma V^{T}$$
- $\Sigma$是对角矩阵
- $U$ 和 $V$ 都是正交矩阵
任何矩阵都可以有奇异值分解,中间是一个对角矩阵,两边是两个正交矩阵
Motivation
行空间 $\in\mathbb{R}^{n}$ 中的标准正交基$v_{1},v_{2},\cdots$,寻找一个变换$A_{m\times n}$,使之变换成列空间 $\in\mathbb{R}^{m}$ 中的一组正交基$u_{1}=Av_{1},u_{2}=Av_{2},\cdots$,即
$$Av_{1} = \sigma_{1}u_{1} \\Av_{2} = \sigma_{2}u_{2}\\ \cdots$$
其中,$\sigma$是伸缩向量,目的是为了是使得$v$也是归一化后的标准正交基
化成矩阵形式即:
$$ A\begin{bmatrix} v_{1} &v_{2} &\cdots &v_{r} \end{bmatrix} = \begin{bmatrix} u_{1} &u_{2} &\cdots \end{bmatrix} \begin{bmatrix} \sigma_{1} && \\ &\sigma_{2} & \\ &&\ddots \end{bmatrix} $$
即
$$AV = U\Sigma$$
$$A = U\Sigma V^{-1}$$
$$AV = U\Sigma V^{T}$$
$V$ 是标准正交的
举个例子,对于矩阵$A=\begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix}$
- 要寻找行空间中的$v_{1},v_{2} \in \mathbb{R}^{2}$
- 要寻找空间中的$v_{1},v_{2} \in \mathbb{R}^{2}$
- 找出归一化系数$\sigma_{1}>0, \sigma_{2}>0$
同时求 $U$ 和 $V$ 太困难了,所以我们想办法消去$U$,先求 $V$
$$ \begin{aligned} A^{T}A &= V\Sigma^{T}U^{T}U\Sigma V^{T} \\\\ &= V\Sigma^{T}\Sigma V^{T} \\\\ &= V\begin{bmatrix} \sigma_{1}^{2} && \\ &\sigma_{2}^{2}& \\ &&\ddots \end{bmatrix} V^{T} \end{aligned} $$
这里最后化简成了对称矩阵$A^{T}A$的对角化形式(特征值分解)$Q\Sigma Q^{T}$,其中$\begin{bmatrix} \sigma_{1}^{2} && \\ &\sigma_{2}^{2}& \\ &&\ddots \end{bmatrix}$是$A^{T}A$的特征值矩阵,$V$是$A^{T}A$的特征向量矩阵
所以如何求 $V$ 和 $U$:
- $A^{T}A$的特征值向量就是$V$
$AA^{T}$的特征值向量就是$U$- $A^{T}A$的特征值就是$\sigma$的平方
这里需要注意的是,通过上述我们无法确定特征向量的符号,在求出$V$后,只能根据$V$的符号来对应$U$的符号,即$Av_{i}=\sigma_{i}u_{i}$
下面来针对上面的矩阵$A=\begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix}$实践一下
$$ A^{T}A = \begin{bmatrix} 4 &-3 \\ 4 &3 \end{bmatrix} \begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix}= \begin{bmatrix} 25 &7 \\ 7 &25\end{bmatrix} $$
标准化后的特征向量是
$$\begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix};\quad \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{bmatrix}$$
得到的特征值是:
$$\lambda_{1} = 32; \quad \lambda_{2} = 18$$
所以可以得到SVD分解中的 $\Sigma$ 和 $V$:
$$ \Sigma = \begin{bmatrix} \sqrt{32} &0 \\ 0 &\sqrt{18}\end{bmatrix};\qquad V=\begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \end{bmatrix} $$
下面用相同的方法去求$U$
$$ AA^{T} = \begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix}\begin{bmatrix} 4 &-3 \\ 4 &3 \end{bmatrix} = \begin{bmatrix} 32 &0 \\ 0 &28 \end{bmatrix} $$
标准化后的特征向量:
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix};\quad\begin{bmatrix} 0 \\ 1 \end{bmatrix}$$
得到 $U=\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$
但是这个$U$是不对的
$AV=\Sigma U$验算不回去,因为同样是特征向量,符号是可以不确定的,而这里选择正的特征向量刚刚好是错误的,所以在指定$V$的特征向量后,对应的$Av_{i}=\sigma_{i}u_{i}$的特征向量符号就出来了
所以这里计算$U$,应该使用$Av_{i}=\sigma_{i}u_{i}$,即:
$$ Av_{1} = \begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{bmatrix} = \begin{bmatrix} 4\sqrt{2}\\ 0 \end{bmatrix} =\sigma_{1}u_{1}=\sqrt{32}u_{1} $$
$$ Av_{2} = \begin{bmatrix} 4 &4 \\ -3 &3 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{bmatrix} = \begin{bmatrix} 0 \\ -3\sqrt{2} \end{bmatrix} =\sigma_{2}u_{2}=\sqrt{18}u_{1} $$
$$ u_{1} = \begin{bmatrix} 1 \\ 0 \end{bmatrix};\qquad u_{2} = \begin{bmatrix} 0 \\ -1 \end{bmatrix};\qquad U=\begin{bmatrix} 1 &0 \\ 0&-1 \end{bmatrix} $$
和上面的错误结果只有符号的差异
再举一个特殊的例子,秩1矩阵$\begin{bmatrix} 4 &3 \\ 8 &6\end{bmatrix}$
矩阵的行空间就是$\begin{bmatrix} 4 \\ 3\end{bmatrix}$的倍数,即所在所在的直线,在这个空间中选择标准基,即$v_{1}=\begin{bmatrix} 0.8 \\ 0.6\end{bmatrix}$
矩阵的列空间就是$\begin{bmatrix} 4 \\ 8\end{bmatrix}$的倍数,即所在所在的直线,在这个空间中选择标准基,即$u_{1}=\frac{1}{\sqrt{5}}\begin{bmatrix} 1 \\ 2\end{bmatrix}$
$$A^{T}A = \begin{bmatrix} 80 &60 \\ 60 &45\end{bmatrix}$$
得到$\lambda_{1}=0,\quad \lambda_{2}=125$
因为秩1,所以选择零空间和左零空间中的标准正交基来构成$U$和$V$
所以最后得到:
$$ A= \begin{bmatrix} 4 &3 \\ 8 &6\end{bmatrix}= \frac{1}{\sqrt{5}}\begin{bmatrix} 1 &2 \\ 2 &-1\end{bmatrix} \begin{bmatrix} \sqrt{125} &0 \\ 0 &0 \end{bmatrix} \begin{bmatrix} 0.8 &0.6 \\ 0.6 &-0.8 \end{bmatrix} =U\Sigma V^{T}$$
31. 线性变换及对应矩阵
线性变换:加法和数乘,线性变换应该保证这两种运算的不变形,即:
$$ \begin{aligned} T(v+w) &= T(v) + T(w) \\\\ T(cv) &= cT(v) \end{aligned} $$
等同于判断:
$$T(cv+dw) = cT(v) + dT(w)$$
举个例子:投影就是线性变换
如果想要了解线性变换对输入空间的影响,只需要了解线性变换对这个输入空间的一组基进行的变换即可
坐标:源自于一组基,$v$的坐标是一组数字:$c_{1},c_{2},\cdots$,表示了$v$由多少个基向量组成,即$v=c_{1}v_{1}+c_{2}v_{2}+\cdots$
平时的话是因为默认存在了标准正交基,即$v=\begin{bmatrix} 3 \\ 2 \\ 4\end{bmatrix}$,但是里面的含义其实是:
$$ v = 3\begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix} + 2\begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix} + 4\begin{bmatrix}1 \\ 0 \\ 1\end{bmatrix} $$